Vol.20:算数の文章題を解くときの子どもたちの頭の中
算数の文章題を解くときの子どもたちの頭の中
小学生が、教科書で学んで単元の内容を「理解した」というのはどういう状態をいうのだろう。このことを、小学3、4、5年生に算数の文章題を解いてもらったデータから考えたい。
この調査では、小学1年生の単元の「ずをつかってかんがえよう」から1題と、小学3年生の単元から7題、合計8題の問題を解いてもらった。問題はごく基本的な問題で、教科書の問題をほぼそのまま使った。
その中から、正答率が低かった問題に焦点をあて、子どもがどのように解答したか紹介しながら「算数の文章題に取り組んでいるときの子どもの頭の中」について考察し、さらにそこから「生きた知識」の性質や習得の仕方について考えたい。
まず、3年生の「あまりのある割り算」の単元から出題した「1まいの画用紙から、カードが8まい作れます。45まいのカードを作るには、画用紙は何まいいりますか。」という問題を見てみよう。3,4,5年生がどのくらい正解できただろうか?
正答率は低く、3年生で41.13%、4年生で48.85%、5年生でも53.90%の子どもしか正答していない。45÷8ではあまりがでてしまう。この文章に書かれていないあまりをどうするか。多くの子どもは、文章の意味をきちんと考え、問いに合わせて答えを書くことができない。「画用紙8まいでは40枚のカードしかつくれない、だからもう1まいよぶんに画用紙がひつようだ。」というように、常識を使って考えることができず、「5まい」と答えている。
別の典型的な間違いは、他の問題と同様、とにかく問題文の数字を思いつく演算に放り込んでしまうタイプのものである。
どちらの解答例でも、計算は正しい。わり算のあまりも、かけ算の繰り上がりもできている。しかし、計算の知識を使って文章で問われている答えを出せないのである。
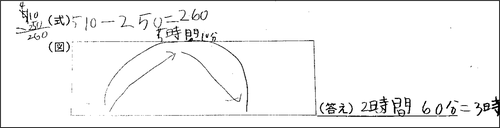
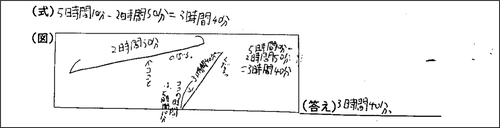
8問の文章題で、もっとも正答率が低かったのは、問題4の「えりさんは、山道を5時間10分歩きました。山をのぼるのに歩いた時間は、2時間50分です。山をくだるのに歩いた時間は、何時間何分ですか。」である。この問題も3年生の単元なのに、学年別正答率は3年生が17.73%、4年生で25.95%, 5年生でも53.90%だった。
この問題を解けない子どもたちは、どのような間違い方をしているのだろうか?
まず、画用紙の問題と同様、問題文を読み取れず、式にできない子どもたちがいる。
計算は、時間と分に分け、それぞれ別に足し合わせている。特にこの子どもは、この計算方法では分のほうが60分になるので、答えは8時間とするべきなのだが、7時間60分と書いて見直さず、そのままである。
「510-250=260」という解答を書いた子どもは、明らかに時間の単位がわかっていない。5時間10分をそのまま510にしてしまっていることから、1時間は100分と思っているようである。しかし、答えに注目すると、260分を2時間60分として、3時間と書いている。つまり、1時間は60分ということを知らないわけではなく、ここでは使えている。
その次の誤答では、5時間10分、2時間50分をきちんと分に変換できている。しかし、せっかく310-170=140分と正しく計算できたのに、答えを書くときに1時間40分と、10進法を使って書いてしまっている。
つまり、あることを「知っている」ことと「使って問題解決ができる」ことは同じではないのである。
子どものこのような間違いは、知識の性質について大事なことを教えてくれる。単元の内容が「わかった」と「わからない」はあるところを境界にして、パッとわかれるわけではなく、連続的につながるものなのである。「5時間10分は、何分?」と聞き、「310分!」と答えられると、大人は安心して、「時間の単位変換はOKね」と思ってしまう。しかし、「1時間は60分」と頭で知っている状態から、その知識が使い込まれて、自然とその変換が身体の一部になっていないと、その知識が文章題を解く過程で使えない。思わず140分の答えを「1時間40分」に書いてしまう。言い換えればこのような誤答をする子どもたちは、だいたいわかっているのだが、時間の単位を使って問題を解決する練習が足りていないので、知識が身体化されておらず、頭でとどまってしまっているのである。
この誤答をした子どもは、分単位への変換する必要があることも思い出せていない。時間の60進法もわかっていないのではないか。
文章の意味を考えず、やみくもに計算をして答えを出そうという方略は、この誤答にもっとも顕著に表れている。この解答をした子どもは、時間のほうは5-2で3時間を出し、分のほうは、なんと、10-50ができないから50-10にしてしまっている。これはこの時間の問題に限らず、繰り下がりがある引き算全般に見られる方略である。
これらの誤答には、メタ認知・批判的思考の未熟さも反映されている。ちょっと見直して自分の正解をチェックすれば正答できる知識はもっているのに、答えを振り返って見直すことをせず、とりあえず答えがでたらそれを書き、そこで終わってしまう。
これはメタ認知・批判的思考の問題であるが、その背後には、算数の文章題に対する子どもたちの認識もあると思う。算数の文章題は意味があってそれを考えることに意義があるということを子どもたちは理解できておらず、問題にある数字に対して知っている式に入れてとにかく答えを出せばよいと多くの子どもは思っている。だから答えがヘンでないか、ほんとうにこれでよいのか、チェックをすることをしないのである。
算数の授業で、子どもたちは計算のしかたや単位変換のしかたなど、実に多くのことを学ばなければならない。しかし、それらはただ「やりかたをおぼえる」ことになってはならない。なんのために算数を学ぶのか。それを子どもたちが感じられる授業が必要だ。同時に、学んだ単元の内容を「どう使うか」を学ばなければならない。そのためには学んだ内容をその単元の終わりで「もう学習が済んだ内容」にせず、実生活に結びついたさまざまな場面で繰り返し使う場面をつくることも大事である。
知識は使わなければ忘れてしまう。3年生で習った単元を、その後使う機会がないのに、1年後に、「去年もうこの単元は学習したからこの内容は知っているはず、この計算はできるはず」という前提で新しい単元に入ることは、人は(大人でも)使わない知識はすぐに忘れる、という記憶の大原則に反しているのである。
慶応義塾大学教授 今井むつみ